Welcome in the second part of this first journey in C code optimization (first because I hope to show also FFT). We started in this post with several optimization techniques applied to the Matrix Multiplication, in particular:
- monodimensional pointers (a[n*w+m] in place o a[n][m])
- indeces precomputation (applied to monodimensional pointers)
- physical transposition of the second matrix to allow a cache contiguous access.
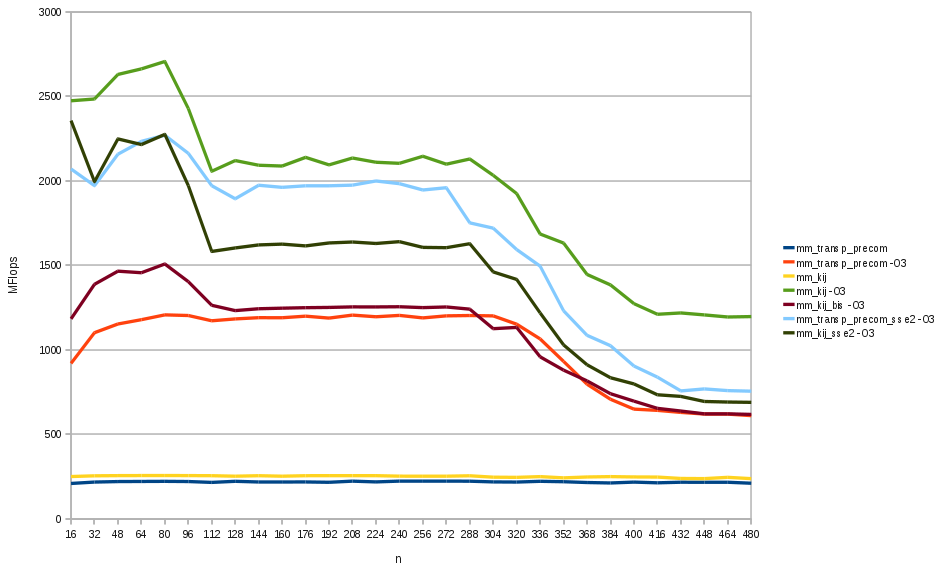
The result was interesting, since in the graph we could see the impact of the various levels of cache (there were steps in the FLOPs chart where instances of the multiplication fitted the L1 cache, L2 cache and L3 cache).
In this post we’ll proceed further and obtain an implementation that is good for every size of the matrices.
Vectorization
Since summation is associative, we can change the order of the loops. If we consider this code:
void mm_1_kij(double *m1, double *m2, double *m3, int a, int b, int c) {
double *mb;
double ma;
for (int i=0; i<a; i++) {
mb = m2;
for (int k=0; k<b; k++) {
ma = *m1++;
for (int j=0; j<c; j++) {
m3[j] += ma * mb[j];
}
mb += c;
}
m3+=c;
}
}and try to compile it, it is 10% faster in -O0 version (about 250 MFlops vs 220 MFlops), but it is tremendously faster in -O3 version (Fig 2.). Infact -O3 actives the auto-vectorization mode and if we compile also with -ftree-vectorizer-verbose=2 flag, we see that the inner loop has been vectorized:
mm_1.c:258: note: LOOP VECTORIZEDLet’s note that a similar code, like
void mm_1_kij_bis(double *m1, double *m2, double *m3, int a, int b, int c) {
double *mb;
double ma;
for (int i=0; i<a; i++) {
mb = m2;
for (int k=0; k<b; k++) {
for (int j=0; j<c; j++) {
m3[j] += *m1 * mb[j];
}
mb += c;
m1++;
}
m3+=c;
}
}which also is auto-vectorized, reachs lower performances (even if better than mm_1_transp_precom which is not auto-vectorized).
But what is vectorization? Some processors (almost all CPUs of normal PCs) support special extensions of the x86 instruction set with extra functionality. In particular MMX, SSE, SSE2 (but also 3DNow!, SSE3, SSSE3, SSE4, AVX) are special instructions that allow to execute the same instruction on multiple operands (so they are SIMD (Single Instruction Multiple Data) operations) In particular SSE is an instruction set operating on eight 128-bit registers, used to performe the same operation on 4 32-bit floating point numbers stored in them. SSE2 expands to 16 the number of registers and admits also to perform operations on two 64-bit double precision floating point numbers, two 64-bit long integers, four 32-bit integer, eight 16-bit short integer or 16 8-bit char.
And how can we use this processor ability? It is quite simple; we have to include in the C source the headers with the intrinsics that we need and use them into the code. Here a list of the right headers which we must include to use some of this instruction set in programs:
| include | instruction set |
| #include <mmintrin.h> | MMX |
| #include <xmmintrin.h> | SSE |
| #include <emmintrin.h> | SSE2 |
| #include <pmmintrin.h> | SSE3 |
| #include <tmmintrin.h> | SSSE3 |
| #include <smmintrin.h> | SSE4 |
| #include <ia64intrin.h> | IA-64 |
So let’s modify mm_1_kij and mm_1_transp_precom to use the SSE2 instruction (note, my code here is not general, it requires c be divisible by two):
void mm_1_kij_sse2(double *m1, double *m2, double *m3, int a, int b, int c) {
__m128d ma, *mb, *mc = (__m128d *) m3;
int t1,t2;
int c_2 = c>>1;
for (int i=0; i<a; i++) {
mb = (__m128d *) m2;
for (int k=0; k<b; k++) {
ma = _mm_load1_pd(m1++); //k*a+i
for (int j=0; j<c_2; j++) {
mc[j] = _mm_add_pd(mc[j], _mm_mul_pd(ma, mb[j]));
}
}
mc+=c_2;
}
}
void mm_1_transp_precom_sse2(double *m1, double *m2, double *m3, int a, int b, int c) {
double T[c*b];
__m128d *ma, *mb;
int t1,t2;
for (int i=0; i<b; i++) {
t1=i*c;
t2=i;
for (int j=0; j<c; j++, t2+=b , t1++)
T[t2] = m2[t1];
}
int b_2 = b>>1;
__m128d parz;
double temp[2];
for (int i=0; i<a; i++) {
ma = (__m128d *) (m1+(i*b));
for (int j=0; j<c; j++) {
mb = (__m128d *) (T+(j*b));
parz = _mm_set1_pd(0.0);
for (int k=0; k<b_2; k++) {
parz = _mm_add_pd( parz, _mm_mul_pd(ma[k], mb[k]) );
}
_mm_store_pd( temp, parz);
*m3++ = temp[0]+temp[1];
}
}
}We need to compile this code with -msse2 option (and we must include emmintrin.h in the source). The velocity increase for mm_1_transp_precom_sse2 is not bad, it is almost twice faster than its non-vectorized version, but still is slower than mm_1_kij -O3 which has been auto-vectorized by the compiler (Fig 2.).
mm_1_kij_sse2 is worst than mm_1_transp_precom_sse2. -O3 auto-vectorization wins this battle but we can use another powerful weapon: loop unrolling.
Loop unrolling
A problem of loops is that after each execution of their body the CPU must evaluate the termination condition. An if has two outcomes (true or false) so there are two possible instructions executed after the if. This is a branch in the execution tree of the program and the CPU as a specific unit to predict the outcome of the branch: the branch predictor. It aims to maintain the execution pipeline of the CPU as full as possible and reducing the number of if helps the predictor.
If we repeat the body of the inner loop more than once, adjusting the increment and the termination condition in the header, we reduce the number of the jump, improving the performance of the program (since the processor pipeline should be better used). Trying this code
void mm_1_kij_sse2_unroll8(double *m1, double *m2, double *m3, int a, int b, int c) {
__m128d ma, *mb, *mc = (__m128d *) m3;
int t1,t2;
int c_2 = (c>>4)<<3;
for (int i=0; i<a; i++) {
mb = (__m128d *) m2;
for (int k=0; k<b; k++, mb+=c_2) {
ma = _mm_load1_pd(m1++); //k*a+i
for (int j=0; j<c_2; j+=8) {
mc[j] = _mm_add_pd(mc[j], _mm_mul_pd(ma, mb[j]));
mc[j+1] = _mm_add_pd(mc[j+1], _mm_mul_pd(ma, mb[j+1]));
mc[j+2] = _mm_add_pd(mc[j+2], _mm_mul_pd(ma, mb[j+2]));
mc[j+3] = _mm_add_pd(mc[j+3], _mm_mul_pd(ma, mb[j+3]));
mc[j+4] = _mm_add_pd(mc[j+4], _mm_mul_pd(ma, mb[j+4]));
mc[j+5] = _mm_add_pd(mc[j+5], _mm_mul_pd(ma, mb[j+5]));
mc[j+6] = _mm_add_pd(mc[j+6], _mm_mul_pd(ma, mb[j+6]));
mc[j+7] = _mm_add_pd(mc[j+7], _mm_mul_pd(ma, mb[j+7]));
}
}
mc+=c_2;
}
}
void mm_1_transp_1idx_sse2_unroll8(double *m1, double *m2, double *m3, int a, int b, int c) {
double T[c*b];
__m128d *ma, *mb;
int t1,t2;
for (int i=0; i<b; i++) { // m2 b x c, T c x b
t1=i*c;
t2=i;
for (int j=0; j<c; j++, t2+=b , t1++)
T[t2] = m2[t1];
}
int b_2 = b>>1;
__m128d parz, r1, r2, r3, r4, r5, r6, r7, r8;
double temp[2];
for (int i=0; i<a; i++) {
ma = (__m128d *) (m1+(i*b));
for (int j=0; j<c; j++) {
mb = (__m128d *) (T+(j*b));
parz = _mm_set1_pd(0.0);
for (int k=0; k<b_2; k+=8) {
r1 = _mm_mul_pd(ma[k], mb[k]);
r2 = _mm_mul_pd(ma[k+1], mb[k+1]);
r3 = _mm_mul_pd(ma[k+2], mb[k+2]);
r4 = _mm_mul_pd(ma[k+3], mb[k+3]);
r5 = _mm_mul_pd(ma[k+4], mb[k+4]);
r6 = _mm_mul_pd(ma[k+5], mb[k+5]);
r7 = _mm_mul_pd(ma[k+6], mb[k+6]);
r8 = _mm_mul_pd(ma[k+7], mb[k+7]);
r1 = _mm_add_pd(r1, r2);
r3 = _mm_add_pd(r3, r4);
r5 = _mm_add_pd(r5, r6);
r7 = _mm_add_pd(r7, r8);
r1 = _mm_add_pd(r1, r3);
r5 = _mm_add_pd(r5, r7);
r1 = _mm_add_pd(r1, r5);
parz = _mm_add_pd( parz, r1);
}
_mm_store_pd( temp, parz);
*m3++ = temp[0]+temp[1];
}
}
}we see that without compiler optimization loop unrolling is good for mm_kij_sse2, but not very much for mm_transp_precom_sse2 unless unroll a lot for cycles. With the -O3 flag we manage to do better than mm_kij -O3 for small matrices and get the same performance for matrices with n smaller than 280. After this point we still can not go faster than the auto-vectorized code.
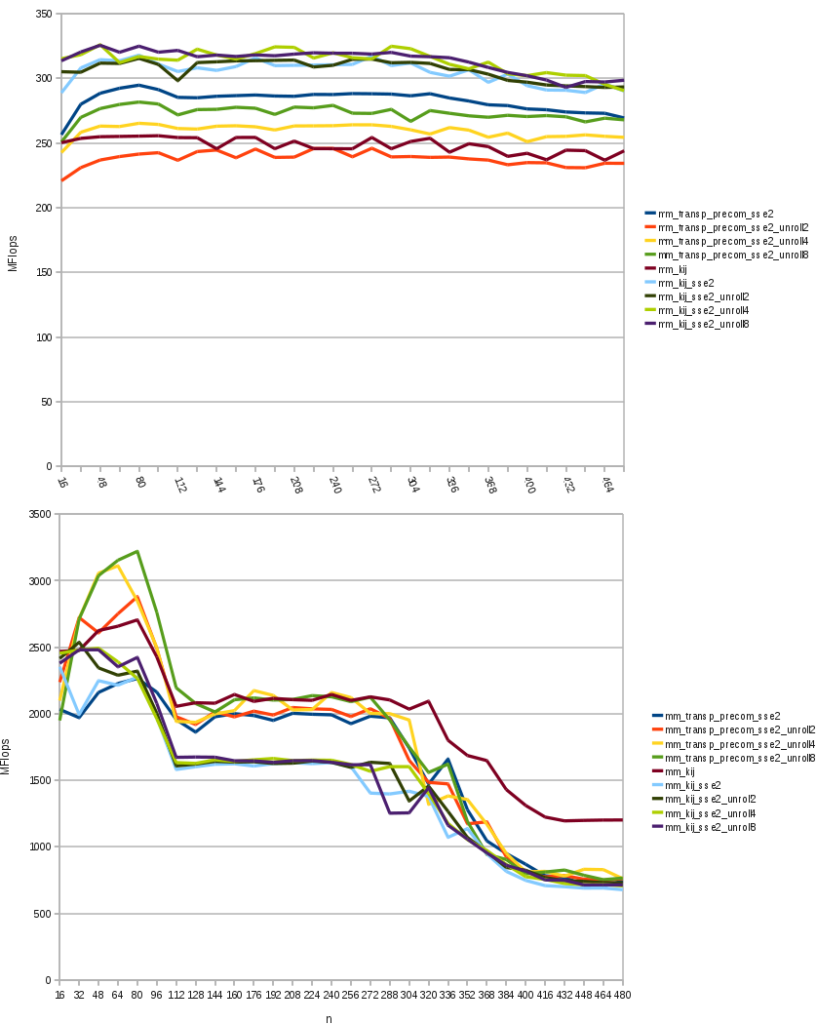
is very fast for matrices 80×80, but still mm_kij -O3
is the fastest for big matrices.
The -O3 already performs loop unrolling in simple loops, so we shouldn’t do it unless the if body has more the one instruction or as some non-trivial complexity. Now it’s time for the last assault to the -O3 power!
Cache friendly computation
When we deal with small matrices (i.e. when we work in cache L1), we can reach 3.2 GFlops, since all data needed by the computation is near the processor. We could divide the matrices in chunks smaller than L1 cache and use them as much as we can.
#define CHUNK 8
void mm_1_transp_1idx_sse2_cache(double *m1, double *m2, double *m3, int a, int b, int c) {
double T[c*b];
__m128d *ma, *mb, mt;
double *mc;
int t1,t2;
for (int i=0; i<b; i++) {
t1=i*c;
t2=i;
for (int j=0; j<c; j++, t2+=b , t1++)
T[t2] = m2[t1];
}
int b_2 = b>>1;
__m128d parz;
double temp[2];
for (int j=0; j<b_2; j+=CHUNK) {
for (int i=0; i<a; i+=CHUNK) {
for (int k=0; k<c; k+=CHUNK) {
ma = (__m128d *) (m1 + i*b + j*2);
for (int i1=0; i1<CHUNK; i1++, ma+=b_2) {
mb = (__m128d *) (m2 + k*b + j*2);
mc = m3 + (i+i1)*c + k;
for (int i2=0; i2<CHUNK; i2++, mb+=b_2, mc++) {
mt = _mm_set1_pd(0.0);
for (int i3=0; i3<CHUNK; i3++) {
mt = _mm_add_pd(mt, _mm_mul_pd(ma[i3], mb[i3]));
}
_mm_store_pd( temp, mt);
*mc += temp[0] + temp[1];
}
}
}
}
}
}We obtain what we were searching for: there are no more influences of the memory hierarchy, the program always runs in L1, for every matrix order.
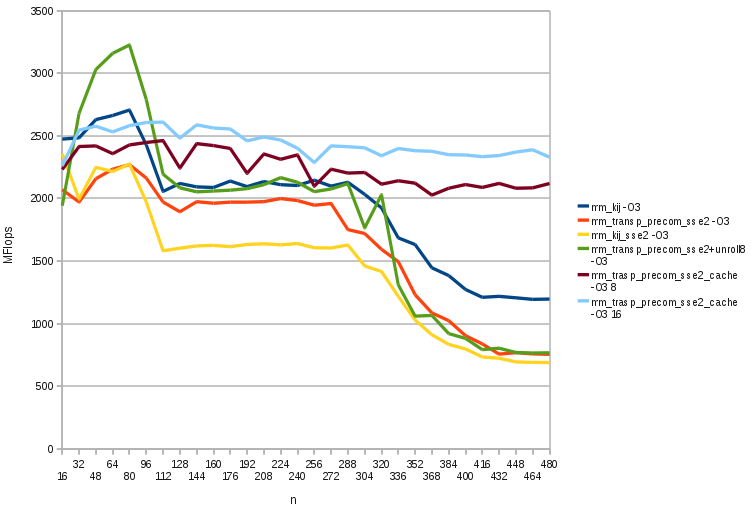
Finally, note than in any of these graphs the timing difference between an algorithm and its -O3 version is about x10: this is due to the efficient prefetch of data inserted in the code by the -O3.
The code genereted by -O3 has code that while your for loop multiplies the first 2 chunks is already loading the next chunks, so at the end of the first chunk multiplication immediately starts the second one. Instead in the -O0 version we don’t put such prefetch operations and would be very interesting to know how to do it.
Other features
In this post and the previous we try very hard to optimize the classic O(n3) matrix multiplication algorithm. This is not the best possible implementation, we can still prefetch data (than we delegated to the -O3), use wider SIMD instruction sets, parallelize code with multi-threading.
Prefetch and multi-threading would give great improvements, but they would requires a lot of time for manual implementation and would make the code hard to modify.
Algorithm choice
There exist algorithms asymptotically faster than the classical, the first one is Strassen algorithm that is O(2log27) ≅ O(22.8) in place of O(2log28) = O(23). Imagine the chunk computation implemented in the last paragraph, if we divide A and B both in 2×2 chunks, in classical algorithm we compute 8 multiplication of n/2 x n/2 matrices:
| A11 | A12 |
| A21 | A22 |
| B11 | B12 |
| B21 | B22 |
| A11B11+A12B21 | A11B12+A12B22 |
| A21B11+A22B21 | A21B12+A22B22 |
In Strassen we perform 7 multiplication of n/2 x n/2 matrices and the 4 C chunks are obtained by linear combinations of these 7 submatrices (you can find the combinations in Wikipedia). They require additions of matrices but addition is O(n2), so o(n3) and is a good strategy to reduce the number of operations needed.
The implementation complexity of Strassen is not much greater than classical MM and for big instances it would reduce a lot the execution time. Best known upper bound is O(22.37) but it is bad to implement.
Conclusions
In my opinion in these posts there are more lessons:
- often is better to write a simple algorithm (maybe with some predisposition) and delegate optimization to -O3. In this way you’ll save a lot of time, bugs, readability of the code and future maintenance of the code.
- monodimensional arrays, precomputation of index (compute a multiplication only once and then use more time addition on this term) can help
- if you can make the problem run in cache L1/L2, that are 10 times faster than RAM, you’ll have great performance. In general you need to divide the problem in chunks so that each one fit the cache give you a good speedup, but usually this makes the algorithm more complex. Also the pattern of access of data helps speeds, data shouldn’t be too sparse to exploit the cache.
- computational complexity algorithm can do much more than optimization. You’ll order an array of a million element with a bad mergesort implementation within seconds, while a very optimized insertion sort implementation will take hours to finish the task.
- optimization requires A LOT of knowledge about mathematics, computer architecture (structure of caches, behavior of CPU…), programming techniques, compilers behavior. It’s not a simple matter, you need years to have some good understanding of it and maybe decades to master it. Often it is counter-productive to use it and not always is needed, you should learn when is useful, so be careful in optimize you code (after all with great power comes great responsibility).
You can find the sources of the optimizations in my github, I still have to clear them, but for the moment a leave them available as they are.
https://github.com/zagonico86/my-snippets/tree/main/code-optimization/mm
