I want to share an in depth experiment in code optimization the I did at least ten year ago during my PhD in high performance computing. I offer you to choice between two options: read this post or ignore this post.
If you choose to skip this post your mind will stay safe, tomorrow you’ll wake up in your bed and you’ll believe whatever you want about code optimization.
But if you choose to continue with the reading, you’ll enter in Wonderland and I’ll show you how deep the rabbit hole goes (and you’ll have several headaches and you won’t have the problem to wake up from your bed, because I’ll be already awake coding all night…)
Matrix Multiplication is a well known problem, often used as test case for code optimization and parallelization techniques.
In this post I’m showing the effectiveness of the following techniques:
- -O3 (the most simple and effective 😉 )
- Precomputation of indices in loops
- Loop unrolling
- Vectorization
- Cache friendly code
I’ll show how each of them improves the program performance. In particular I measure the MFlops (millions of floating point operations per second) with PAPI Library, computing n times in a loop in the main a certain multiplication, with a code similar to this:
float real_time, proc_time, mflops;
long long flpops;
float ireal_time, iproc_time, imflops;
long long iflpops;
int retval;
if ((retval=PAPI_flops(&ireal_time,&iproc_time,&iflops,&imflops)) < PAPI_OK) {
printf("Could not initialise PAPI_flops \n");
printf("Your platform may not support floating point operation event.\n");
printf("retval: %d\n", retval);
exit(1);
}
for (t=0; t<n; t++) // here the actual work
mm(m1,m2,m3,a,b,c);
if ((retval=PAPI_flops( &real_time, &proc_time, &flops, &mflops)) < PAPI_OK) {
printf("retval: %d\n", retval);
exit(1);
}
fprintf(stderr, "Size: %d-%d-%d Cycles: %d Real_time: %f Proc_time: %f Total_flops: %lld MFLOPS: %f\n",
a, b, c, prove, real_time, proc_time, flops, mflops);The results have been obtained in a AMD Athlon(tm) Processor LE-1620, 2.6 GHz, with 64 KB cache L1 for data, 64 KB cache L1 for instructions and 1MB cache L2, with Linux 2.6.32-5-amd64 (Debian 2.6.32-41squeeze2) and gcc 4.4.5.
Maybe in the future I’ll compile them again in a modern PC, maybe also considering not only the in-core optimization but also the parallelization optimization (so multi-threading, non-naive algorithms like Strassen, etc…)
Basic Algorithm
Let’s start with the basic algorithm:
void mm(double **m1, double **m2, double **m3, int a, int b, int c) {
for (int i=0; i<a; i++) {
for (int j=0; j<c; j++) {
for (int k=0; k<b; k++) {
m3[i][j] += m1[i][k]*m2[k][j];
}
}
}
}If we compile (without -On flag) we reach about 100 MFlops. Simply compiling with -O3 flag, the improvement is notable: more then 1 GFlops for matrices of order less than 120, 600-800 MFlops for matrices of order less than 350 and about 300 MFlops for bigger matrices (see Fig. 1).
Mono-dimensional pointers
Let’s rewrite the function using mono-dimensional arrays:
void mm_1(double *m1, double *m2, double *m3, int a, int b, int c) {
for (int i=0; i<a; i++) {
for (int j=0; j<c; j++) {
for (int k=0; k<b; k++) {
m3[i*c+j] += m1[i*b+k]*m2[k*c+j];
}
}
}
}The result is slightly better than the previous. Moreover, we can see that the -O3 version is very noisy (as the previous one).
Indeces precomputation
Some offsets in the inner loop are used a lot of times (n times), but they are recompute in each iteration. If we precompute every offset before the cycle we double the MFlops in the -O0 version, since we save O(n3) sums and multiplications used to find the offsets (now we compute only O(n2) offsets).
void mm_1_precomp(double *m1, double *m2, double *m3, int a, int b, int c) {
double *ma, *mb, *mc;
ma = m1;
for (int i=0; i<a; i++) {
for (int j=0; j<c; j++) {
mb = m2+j;
int t = i*c+j;
for (int k=0; k<b; k++, mb+=c) {
m3[t] += ma[k] * *mb;
}
}
ma+=b;
}
}However, the -O3 version has exactly the same performances of mm_1, infact the -O3 flag actives optimizations like indices precomputation.
Make the structures cache friendly
Matrices are saved in memory in row-major (if M is a square matrix of order n, the element M[i][j] is in the memory address M+i*n+j), so computing
Cij = Σk=1 to n Aik * Bkj
gives a lot of cache misses. Infact, while A is accessed by rows, whose elements are in adiacent addresses in memory, B is accessed by columns, so when the program accesses an element in a cycle, in the next cycle he does not find the next one already in cache (unless n is small) and has to load it from RAM. If we transpose B before the multiplication, we can access it in the same way of A (by rows):
void mm_1_transp(double *m1, double *m2, double *m3, int a, int b, int c) {
double T[c*b];
for (int i=0; i<b; i++) // m2 b x c, T c x b
for (int j=0; j<c; j++)
T[j*b+i] = m2[i*c+j];
for (int i=0; i<a; i++) {
for (int j=0; j<c; j++) {
for (int k=0; k<b; k++) {
m3[i*c+j] += m1[i*b+k]*T[j*b+k];
}
}
}
}The improvement is good, expecially in the -O3 execution. In the -O3 line chart (the light green line in Fig 1) of this technique we can see the influence of the memory hierarchy: L1 has 64K, so it can contain about a square matrix of double of order 90, L2 has 1MB, so it can contains a square matrix of double of order 350.
Finally we combine this technique with the previous one:
void mm_1_transp_precom(double *m1, double *m2, double *m3, int a, int b, int c) {
double T[c*b];
double *ma, *mb;
int t1,t2;
for (int i=0; i<b; i++) { // m2 b x c, T c x b
t1=i*c;
t2=i;
for (int j=0; j<c; j++, t2+=b , t1++)
T[t2] = m2[t1];
}
for (int i=0; i<a; i++) {
for (int j=0; j<c; j++) {
t1 = i*c+j;
ma = m1+(i*b);
mb = T+(j*b);
for (int k=0; k<b; k++) {
m3[t1] += ma[k]* mb[k];
}
}
}
}Improvement is good as long has matrices fit L2 memory.
Partial results
Now let’s resume in a graph what we saw so far.
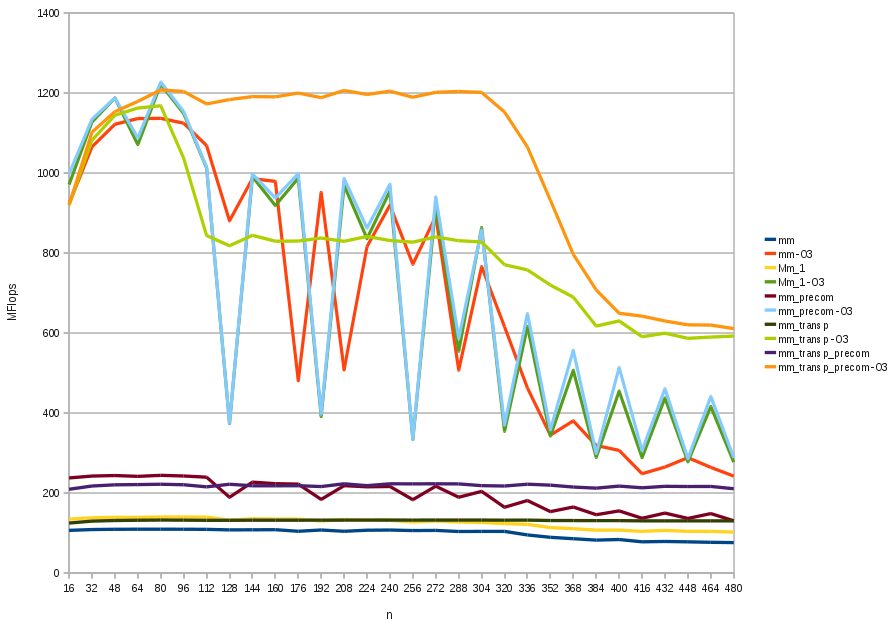
Please note in the graph the following facts:
- -O0 compiled programs are very bad respect to -O3 compiled programs. -O1, -O2 and -O3 enable more and more automatic trasformations of code like precomputation, prefetch of data, loop unrolling, and many other, that allows to maintain the pipeline of the cpu always full during execution.
- In the graph we can see also the footprint of the memory levels L1 and L2. Memory hierarchy notoriously has a pyramidal shape, the near you are to the CPU and the less memory you have but the faster it works. With suitable problems (like matrix multiplication) if communication and computation is optimized opportunely, code can always works at maximum CPU speed; if you see the footprint of memory hierarchy code is not optimized enough.
What’s coming next?
So far so good, but we want to exploit the full FLOPs of the CPU for any matrix size. This post is the first part of my experiment, in the next one there will be the use of vectorized code, the split of the matrices in blocks and loops unrolling, so don’t miss the next part!
Moreover you can find the source code (not yet cleared) in my github.
